General Planar Motion with a Center of Mass Reference - Example Problem 6.7-4

 

A disk of mass m and radius r rolls down an inclined hill as shown in the figure. A force P, which is applied parallel to the inclined surface, resists the motion of the disk. If the disk is released from rest, determine the angular acceleration of the disk if P = 0. Also, determine the minimum force P required to prevent the disk from rolling down the incline. Assume that the disk rolls without slipping. The coefficient of static friction is μ_s.

 

 

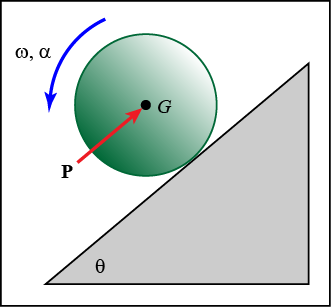
Given:

• ω_o = 0
• Disk (r, m)
• No slip

 

Find: α for P = 0, minimum P for α = 0

 

Video solution:

 

The following video walks you through the solution to this problem. It is suggested that you try solving the problem first and then, if you have difficulties with the solution, watch the video for help.

 

 

Interactive solution:

 

Draw a free-body diagram of the disk. Assume that the disk does not slip on the hill. Click on the figure to see the FBD.

 

Sum the moments about G. Which equation do you obtain?

 

F_fs = (1/2)mrα
F_fs - mg sinθ = (1/2)mr²α
F_fs = (1/2)mr²α