Angular Impulse-Momentum Principle - Example Problem 10.7-4
A 1000-kg satellite is tethered to a 200-kg satellite by a light cable. For the situation shown, the satellites and cable are rotating with an angular velocity of 0.5 rpm. If the larger satellite slowly releases another 10 m of cable, determine the final angular velocity of the system. Treat the satellites as particles. Reconsider the situation, but now take into account the mass moments of inertia of the two satellites. Assume that the larger satellite has a mass moment of inertia about an axis through its mass center that is parallel to the axis of rotation of 500 kg-m2. Likewise, assume the smaller satellite has a mass moment inertia about a parallel axis through its mass center of 10 kg-m2.
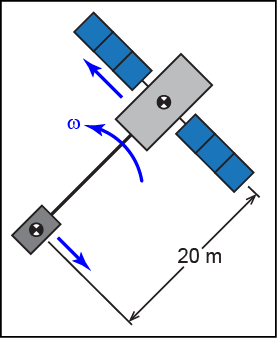
Given:
- mA = 1000 kg
- mB = 200 kg
- L1 = 20 m
- L2 = 30 m
- state 1 = before the tether is extended
- state 2 = after the tether is extended
- ω1 = 0.5 rpm
Find:
- ω2 for a) particle model, b) rigid-body model
Determine the system's center of mass as measured from the mass center of the 1000 kg satellite for state 1 and state 2.
