Applying Newton's Second Law - Example Problem 5.6-9

 

A racecar weighing 3400 lb is racing in the Daytona 500. The track dimensions are as follows:

 

Superspeedway

• 2.5-mile tri-oval
• 40 feet wide
• 12- to 30-foot apron

 

Turns

• Banking: 31 degrees
• Length: 3,000 feet
• Radius: 1,000 feet

 

What is the range of speed that the race car can maintain through a turn without slipping on the track? Assume that the car maintains a constant speed through the turn and neglect the size of the car. Assume that the friction characteristics between the tire and track can be estimated as that between rubber and dry asphalt.

 

 

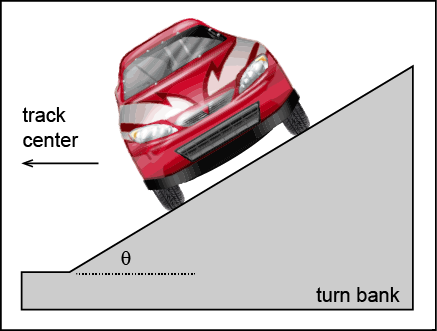
Given:

• W = 3400 lb
• v = constant
• ρ = 1000 ft
• θ = 31^o
• μ_s = 0.9

 

Find:

• v for no slip

 

Video solution:

 

The following video walks you through the solution to this problem. It is suggested that you try solving the problem first and then, if you have difficulties with the solution, watch the video for help.

 

 

Interactive solution:

 

 

Draw 2 free-body diagrams of the car. One for when the car is on the verge of slipping up and one for when it is on the verge of slipping down. Use the n-t coordinate system. The free-body diagrams should show the n-b plane.

 

 

 

 

What is the coefficient of static friction?

 

μ_s =