Plane Curvilinear Motion: Polar Coordinates - Example Problem 3.4-5

 

A robotic arm extends along a path r = (1 + 0.5 cosθ) m. At θ = π/4 rad, (dθ/dt) = 0.5 rad/s and (d ²θ/dt ²) = 0.7 rad/s², find the velocity and acceleration of point A.

 

 

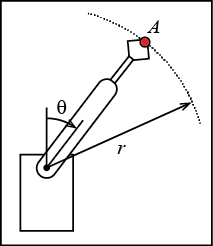
Given:

• r = (1 + 0.5 cosθ) m
• θ = π/4 rad
• (dθ/dt) = 0.5 rad/s
• (d ²θ/dt ²) = 0.7 rad/s²

 

Find:

• v
• a

 

Video solution:

 

The following video walks you through the solution to this problem. It is suggested that you try solving the problem first and then, if you have difficulties with the solution, watch the video for help.

 

 

Interactive solution:

 

We will use polar coordinates in this problem.

 

v = (dr/dt)e_r + r(dθ/dt)e_θ

 

a = ((d ²r/dt ²) - r(dθ/dt)²)e_r + (r(d ²θ/dt ²) + 2(dr/dt)(dθ/dt))e_θ

 

On the figure in your book, draw the x-y and r-θ axes. Click on the figure to see the results.

 

Notice that to calculate the velocity and acceleration of point A, we need to calculate the first and second time derivative of r.

 

Which of the following is the equation for (dr/dt)?

 

(dr/dt) = -0.5 sinθ
(dr/dt) = -0.5(dθ/dt) sinθ
(dr/dt) = 0.5(dθ/dt) sinθ