Impact

 

Impact

 

Impact: When two bodies collide over a very small interval of time and exert relatively large forces on one another. A good example of impact is the game of billiards.

 

 

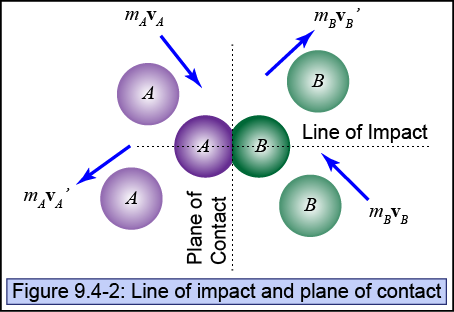
There are two axes that, if identified, may simplify the analysis of the system of colliding particles.

 

• Line of impact: The line drawn between the centers of mass of the two bodies that passes through the contact point.
• Plane of contact: Perpendicular to the line of impact and resides at the contact between the two bodies.

 

 

Coefficient of restitution

 

Energy is generally not conserved during impact (inelastic). Energy is lost due to …

 

• Plastic material deformation
• Heat
• Sound

 

If the bodies stick together after the impact, it is perfectly inelastic. If energy is conserved, the impact is perfectly elastic.

 

A measure of the elasticity of a collision is its coefficient of restitution.

 

• e = 0 (perfectly elastic)
• e = 1 (perfectly inelastic/plastic)

 

Name examples of impacts that are nearly perfectly elastic and perfectly inelastic.

 

 

 

 

Coefficient of Restitution: The ratio between the restorative impulse and the deformation impulse. It also relates the incoming and outgoing particle velocities along the line of impact.

 

e = ∫Rdt/∫Ddt

 

e = ((v_A')_{line of impact} - (v_B')_{line of impact} )/((v_B )_{line of impact} - (v_A )_{line of impact} )

 

 

Impacts of particles are categorized as either; direct central impacts or oblique central impacts.

 

 

Name some examples of direct and oblique central impacts.

 

 

 

 

Analyzing impacts

 

Plane of contact: Assuming no friction, the momenta of the individual particles are conserved along the plane of contact.

 

(v_A' )_{plane of contact} = (v_A )_{plane of contact}

(v_B' )_{plane of contact} = (v_B )_{plane of contact}

 

Line of impact: System momentum is conserved along the line of impact.

 

m_A(v_A )_{line of impact} + m_B(v_B )_{line of impact} = m_A(v_A')_{line of impact} + m_B(v_B ')_{line of impact}

 

e = ((v_A')_{line of impact} - (v_B')_{line of impact} )/((v_B )_{line of impact} - (v_A )_{line of impact} )