Plane Curvilinear Motion: x-y Coordinates

 

Velocity

 

The velocity (v) of a particle is the time rate of change of position (r). Because a plane is 2-D, we need a vector to describe the velocity of a particle.

 

• Velocity vector: v = v_x i + v_y j
• Velocity: v = dr/dt
• Average Velocity: v_ave = Δr/Δt

 

 

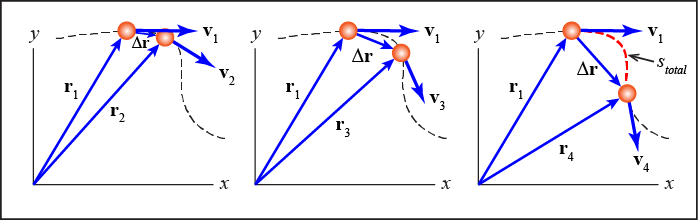
If r = xi + yj, then the derivate of r with respect to time (i.e. the velocity) is equal to the following. Note that we use the product rule to take the derivative.

 

v = dr/dt = (dx/dt) i + x (d i/dt) + (dy/dt) j + y (d j/dt)

 

Is the derivative of a unit direction vector, with respect to time, equal to zero?

 

Yes
No
It depends