Plane Curvilinear Motion - n-t Coordinates
Acceleration
- Acceleration is the time rate of change of velocity.
- If the path of motion is curved, acceleration is not in the same direction as velocity.
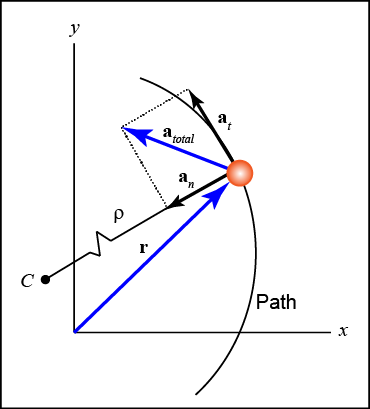
a = (dv/dt) = d(vet )/dt


a = (dv/dt) = d(vet )/dt