Plane Curvilinear Motion: n-t Coordinates - Example Problem 3.3-8

 

A racecar is initially travelling at 75 mph at point A as it enters the S-curve shown. In order to successfully traverse the curve, the racecar driver applies his brakes and decelerates uniformly between point A and B. Point B is located 750 ft down the track from point A. After point B, the racecar driver accelerates uniformly for 850 ft until he returns the vehicle’s speed to 75 mph at point C. If the total acceleration of the vehicle at point A and point C is 10 ft/s², determine

1. the tangential acceleration at point A
2. the total acceleration and velocity at the car approaches point B
3. the radius of curvature of the track at point C.

 

 

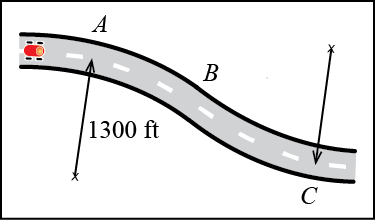
Given:

• v_A = 75 mph = 110 ft/s
• v_C = 75 mph = 110 ft/s
• s_A-B = 750 ft
• s_B-C = 850 ft
• (dv/dt)_A-B = constant
• (dv/dt)_B-C = constant
• a_A = 10 ft/s²
• a_C = 10 ft/s²
• ρ_A = 1300 ft

 

Find:

• a_At
• a_B
• v_B
• ρ_C

 

Video solution:

 

The following video walks you through the solution to this problem. It is suggested that you try solving the problem first and then, if you have difficulties with the solution, watch the video for help.

 

 

Interactive solution:

 

Part a)

 

Since the dimensions of the car are small compared to the dimensions of the track, a particle model is appropriate for the car. Also, information is given and derived about the path taken by the car, therefore, n-t coordinates are a good choice.

 

Which parameter do we need to find in part a) of the problem?

 

a
dv/dt
v²/ρ